Venture capital investment advisory

I advised the shareholders of a company in the tech space on a potential angel investment in a startup that was structured as a convertible discount note. Such instruments are debt, and are therefore senior to stock, but function effectively as equity since the notes will convert into shares at a qualified financing event or maturity.

This transaction was unusual since the founders held a small amount of common stock (relative to the number of shares that would likely convert from the note) and also participated as investors themselves in the convertible financing, something akin to founders preferred stock. This, among other terms, made the transaction founder friendly. On the other hand, my client was offered a board seat, something not typically given to angels, and there were strategic benefits as well.

My role including providing the investor with valuation advice (based on EBITDA or sales multiples, discounted cash flow analysis, etc.), modeling of the deal and negotiation for more favorable terms.

Key convertible discount note terms

• Conversion discount – typically 15% to 25%. A higher discount means convertible note investors obtain shares at a lower price at a qualified financing event, e.g. the issuance of preferred stock to a VC fund.
• Interest rate – as debt instruments, notes earn interest which accrues to the principal balance rather than being paid in cash. Interest rates fluctuate but a coupon of 4% to 6% can be considered standard.
• Term – terms vary according to the objective of the financing. A bridge financing may be structured as short-term note, for example 12 months, although an early stage startup will generally need more time, 18 to 24 months, to close a subsequent round.
• Valuation cap – early stage deals often feature a valuation cap to protect investors under the circumstance that the startup closes a round at a high valuation; without a cap, the notes would convert into a relatively small share of the company, potentially unfair given that the note holders have taken on more risk.
• Liquidation preference – note holders usually convert into the same series of preferred stock that's issued to investors in a qualified financing round, and if a subsequent liquidation event occurs (e.g. the startup is acquired) will receive full payment of the purchase price and unpaid dividends of their preferred stock (1x preference) before the common shareholders may receive proceeds.
• Multiple or participating liquidation preference – in some more investor-friendly deals, convertible note investors may hold the right to receive a multiple liquidation preference (e.g. 2x) under a liquidation event, and/or hold a "participating" preference where in addition to receiving repayment (or multiple thereof) on their preferred stock they also receive an additional payout in proportion to their shareholding, i.e. a "double dip."
• Conversion at maturity – conversion at maturity may be mandatory or alternatively at the option of investors, who may choose to hold their notes and continue accruing interest or with the expectation of note redemption or subsequent conversion or liquidation event (e.g. bankruptcy).

Cap table modeling

In order to understand the potential returns on invested capital, I modeled the company's cap table across various scenario. In the below scenario, I assumed a $1 million angel investment in a convertible note offered with a 30% discount and a $5 million liquidation cap where a $3 million Series A financing is subsequently closed at a $10 million pre-money valuation.

In this scenario, the angel investor's note will convert into shares worth $2.1 million and 12% of the company, yielding a return of 2.1x invested capital. I also presented IRRs in complement to MOIC (multiple on invested capital).

Sensitivity analysis

I modeled the value, number of shares, shareholding and MOIC at conversion for various scenarios with varying transaction terms (discount, valuation cap, etc.) and sensitivities according to the potential pre-money valuations at which the Series A round would be closed.

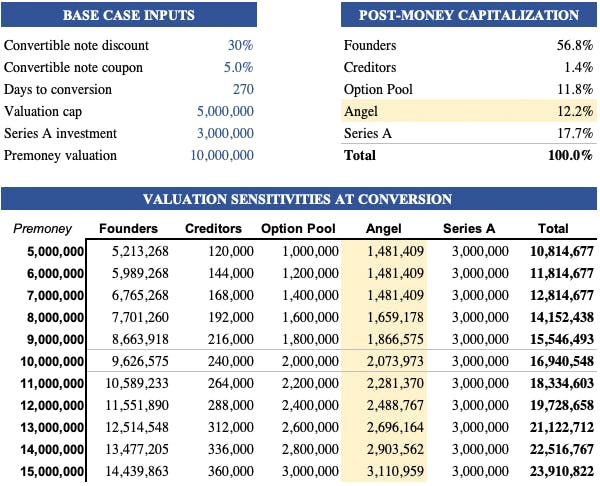
Note that the value of the angel investor's shares at conversion is fixed when the pre-money valuation of the qualified financing is at or below the discounted valuation cap. In the above, the value of the conversion shares is fixed up to a pre-money financing of $7.1 million since the notes carry a 30% discount and a $5 million valuation cap ($5 million is $7.1 discounted by 30%).

I modeled the scenarios using the most founder-friendly (i.e. worst case for investors) pre-money method. The VC will no doubt push for a percentage-ownership method or perhaps compromise to a dollars-invested method, with both scenarios providing better outcomes to my client (at the founder's expense).

I also worked with my client's business development director and counsel as we advanced in due diligence and negotiation of the convertible note purchase agreement.